Bąk symetryczny już bez poślizgu

Notka krótka, techniczna. Nikt nie rozumie o co mi idzie z tym moim nierozumieniem „bez poślizgu”. Tak to już jest . Samotność długodystansowca. Wyjaśnię więc jak ja to widzę. Przypomnę fabułę: rozważamy bąk swobodny, symetryczny. Do tego bąka często podręczniki dodają obrazki dwóch stożków: „stożek ciała” i „stożek przestrzeni”. Pisałem o tym w poprzedniej notce Precesje, nutacje, stożki czyli Feynman nie na żarty i bez poślizgu. Pisałem i pokazywałem obrazki tych stożków. Dziś pokażę obrazek z jeszcze innego podręcznika, mianowicie Schaub, Junkins „Analytical mechanics of space systems”. Pierwsze, wstępne wydanie można sobie ściągnąć z sieci - ale ten pdf jest rąbnięty. W pierwszym wydaniu w tytule jest „aerospace”, w drugim już tylko „space”

Będę się opierał na pierwszym wydaniu - interesujący nas Rozdział 4 można ściągnąćstąd. Na str. 136 znajdujemy tam nasze stożki:

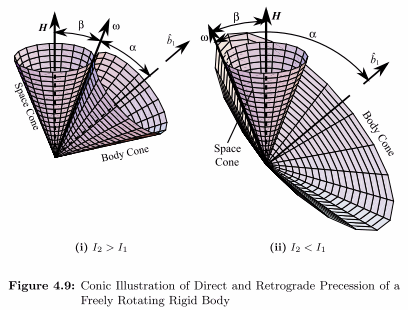
Skoncentruję się na tym lewym obrazku, odpowiada on przypadkowi bąka podłużnego, gdy moment bezwładności względem osi symetrii jest mniejszy od dwu pozostałych, równych sobie momentów. Skoncentruję się na tym lewym, bo jakoś łatwiej nam wyobrazić sobie stożek ciała toczący się po stożku przestrzeni z zewnątrz. Mi w każdym razie łatwiej, a Synge i Griffiths w swoim podręczniku też to zauważają, że łatwiej nam poczuć stożek toczący się po drugim, niż stożek toczący się w drugim.

Co to za stożki? Skąd się wzięły? Czemu się toczą?

Literka H na obrazku, to nasz L – wektor krętu. Jest on stały w przestrzeni, co do wartości i zwrotu, bowiem nasz bąk jest swobodny – prawo zachowania krętu.

Dalej mamy wektor prędkości kątowej ω. Kąt między tymi dwoma wektorami oznaczony jest literką β . Co o tym kącie wiemy?

W układzie ciała Lma składowe (I_Xω_X, I_Yω_Y, I_Zω_Z). My umówiliśmy się, że u naszego bąka osią symetrii jest oś trzecia, zatem I_Y= I_X, Schaub i Junkins przyjmują I_Y= I_Z – nie będziemy zmieniać naszych oznaczeń. Długość wektora L (pogrubione) oznaczmy przez L (nie pogrubione):

L² = I_X²ω_X²+ I_Y²ω_Y²+ I_Z²ω_Z².

Wektor ω ma składowe (ω_X, ω_Y, ω_Z). Jego długość oznaczmy literką ω. Cosinus kąta między dwoma wektorami to ich iloczyn skalarny podzielony przez iloczyn długości. Zatem

cos β = ( I_Xω₁²+ I_Yω_Y²+ I_Zω_Z²)/(Lω ) = ( I_X(ω_X²+ ω_Y²) + I_Zω_Z²)/(Lω )

W notce Precesja symetryczna z równań Eulera wywnioskowaliśmy, że ω_Z jest stałe, (ω_X²+ ω_Y²) jest także stałe. Zatem i kąt β jest stały. Wektor prędkości kątowej ω obiega wektor L pod stałym kątem – zatacza więc ładny stożek. Na obrazku stożek ten jest z napisem „Space cone” - stożek przestrzeni. Tak to się przyjęło nazywać.

Wektor jednostkowy wzdłuż osi symetrii ciała na obrazku oznaczony jest literką b₁. W notce Dwa punkty widzenia - próba pogodzenia my oznaczyliśmy go literką k - i tak będziemy oznaczać. Kąt między wektorem ω a wektorem k oznaczony jest na obrazku literką α . Wektor k ma (w układzie ciała) składowe (0,0,1). Stąd

cos α = ω_Z²/ω

Zatem i ten kąt jest stały. Mamy więc powód do narysowania drugiego stożka „Body cone” - stożek ciała.

Z notki Dwa punkty widzenia - próba pogodzenia wiemy, że wektory L, ω, k leżą w jednej płaszczyźnie, i że wektor ω obraca się wokół L z prędkością kątową L/I_X, natomiast ω obraca się wokół k z prędkością kątową ω_p = (IZ/IX-1)ω_Z . Na lewym obrazku mamy I_Z<I_X, zatem ωp jest ujemne. Te dwa obroty są więc przeciwbieżne.

Teraz moje „bez poślizgu”. Jak ja to widzę? Zamiast obracać oś k i wektor ω wokół wektora krętu L, ustalmy L, ω, k i obracajmy stożki wokół ich osi. W końcu co nam szkodzi?

Prawy stożek, stożek ciała, obracajmy z prędkością kątową ω_p, lewy stożek obracajmy z prędkością kątową L/I_X.Ponieważ oba stożki stykają się wzdłuż ω, pojawia się pytanie: czy będą się obracać nie ślizgając się jeden po drugim?

Miło, że obracają się w przeciwnych kierunkach, ale czy obracają się z takimi jak trzeba prędkościami? Obwód góry lewego stożka jest proporcjonalny do promienia r, obwód prawego do promienia R – na obrazku poniżej:

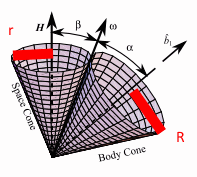
Oznaczając przez h wysokość, mamy

r= h sin β

R= h sin α

Stąd r/R = (sin β)/(sin α)

By nie było ślizgania musi być, że stosunek długości obwodów jest odwrotnie proporcjonalny do częstotliwości obrotów. Ale czy tak jest?

Synge i Griffiths to właśnie wyliczają w swojej książce, zresztą łatwo jest wyliczyć samemu. Znamy cosinusy, stąd obliczamy sinusy, dzielimy, i porównujemy ze stosunkiem częstości obrotów. No i – jest tam trochę manipulacji symbolami, łatwo się pomylić - wychodzi jak trzeba. Możemy zatrzeć ręce i pójść dalej – już bez poślizgu.

W następnej notce, po drodze do gajki Dżanibekowa, zajmiemy się „stabilnością”. O co tu idzie i czy ma to dla nas znaczenie? (nie ma).